ご覧いただきありがとうございます。ここでは、情報を記憶できる最も基本的な回路構成であるフリップフロップについて、ざっくりと説明させていただきます。電子回路において情報を記憶する、とはどういう仕組みで実現されているのかがわかると思います。マイコンによる演算やメモリへの記録なども、このフリップフロップの仕組みを無数に実装することで実現しています。
NANDゲート
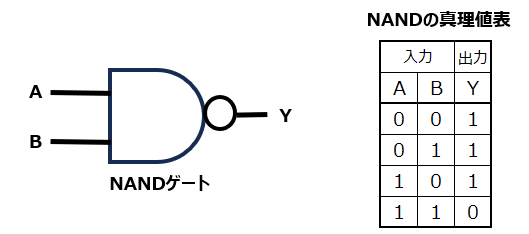
まずはNANDゲートというものについて説明いたします。2つの入力AとBがあり、その演算結果をYとしています。AとBが両方とも1の時はYは0、それ以外はYは1になります。AとBが両方とも1の時に1になるのがAND(論理積)になりますが、その反転ということでNAND(Not AND、否定論理積)となります。物理的には1は電圧が高い(電源電圧と同じ等)、0は電圧が低い(GNDレベル等)という状態となります。
NANDを使ったフリップフロップの構成
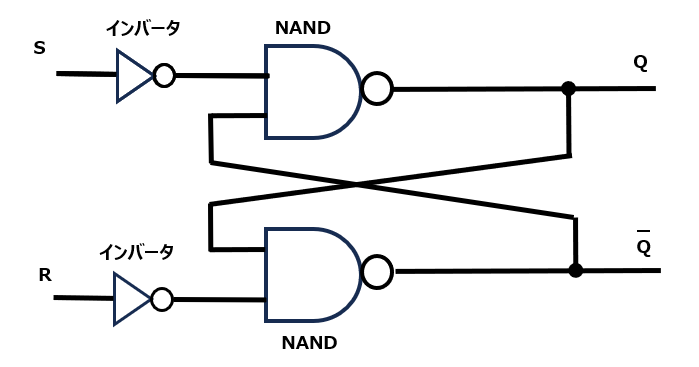
NANDゲートとインバータを使ってこのような回路を組みます。この回路をフリップフロップといいます。一方のNANDの出力を他方の入力に戻しているところがややこしそうに見えますね。インバータは入力の1と0を反転させて出力するもので、物理的な構成は「CMOSの動きをイメージしよう」で解説しているようにMOSFETで構成することができます。NANDも同様にMOSFETで構成できます。上下対称の回路になっていますが、ここでは入力の一方をS、もう一方をRとし、出力はQとQ#としています。(図ではQの上に線を書いていますが文章では表現が難しいので代わりにQ#と表現しました。以降も同様です)SはSet、RはResetから来ており、後述しますがフリップフロップに1をセットする、0にリセットする、というような意味になります。出力をQとしているのは、トランジスタの出力が一般的にQと表現されることに由来しています。
フリップフロップに情報を記憶させる
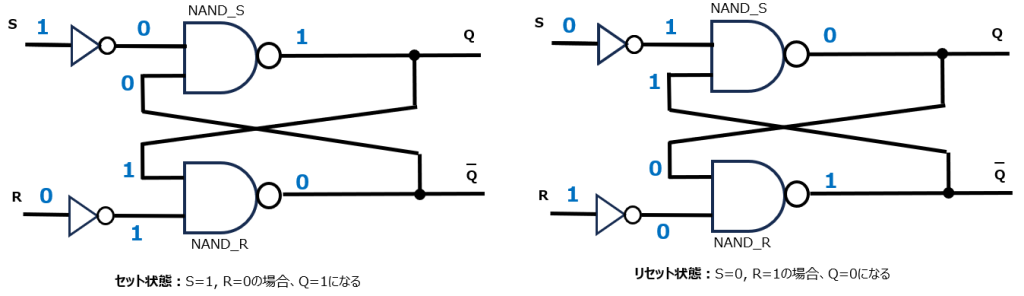
では早速フリップフロップに入力してみましょう。左図(セット状態)ではS=1、R=0を入力し、NANDの真理値表に従ってそれぞれの場所が1か0のどちらになるかを記載しました。一方右図(リセット状態)では、S=0、R=1としています。次にそれぞれについてS=R=0を入力するとどうなるでしょう。
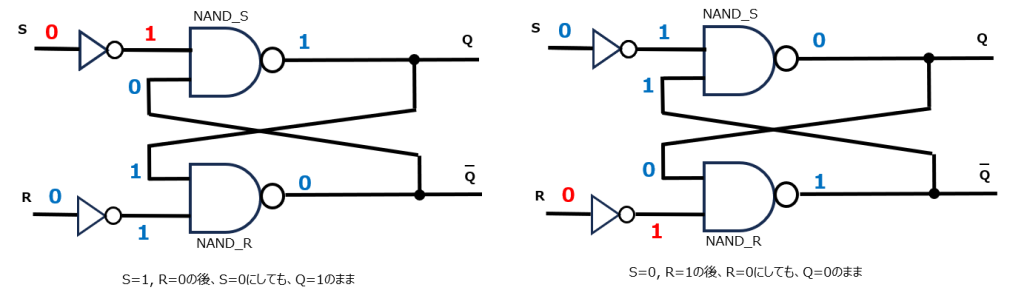
セット状態では元々R=0なのでSだけ1から0に変更します。NANDの真理値表によると、S側のNANDは入力が変わっても出力は1のまま変わりません。同様にリセット状態からはRだけ1から0に変更しましたが、R側のNANDの出力は1のままです。ここで興味深い事実に気がつきます。左右どちらも入力はS=R=0であるにも関わらず、出力は異なっています。S=R=0にする前の状態を覚えていて、その状態を維持しているのです!これは情報を記憶している、ということができるでしょう。なお、いずれの場合もQとQ#は反転の関係になっています。
S=1,R=1は禁止
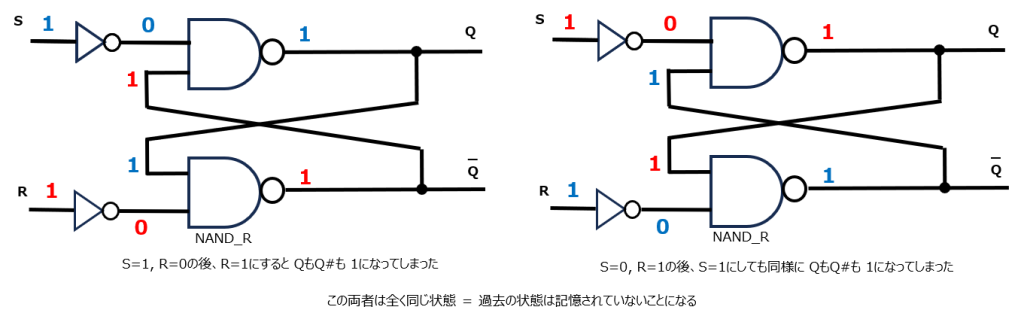
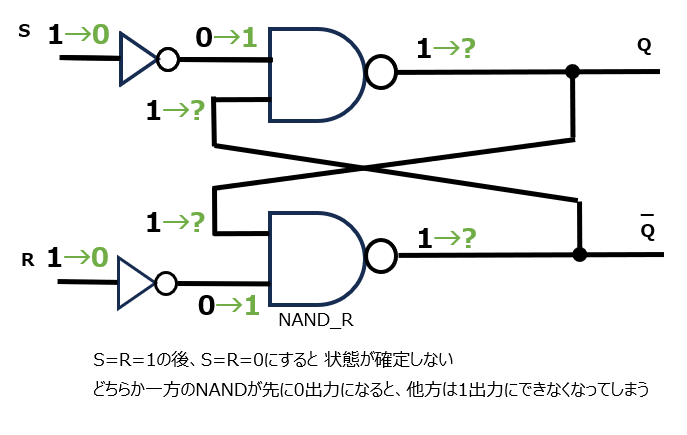
ところが、S=R=1を入力すると困ったことが起きます。セット状態からR=1に変更すると、R側のNAND出力は1に変わってしまいます。リセット状態からも同様です。そうなるとどちらのNANDも1を出力している状態になります。よく見るとこの両者は同じ状態になっています。つまり、過去にセット状態だったのかリセット状態だったのかという記憶が無くなってしまっているのです!こうなると記憶する回路にならなくなってしまいます。さらにこの後S=R=0(保持)とするとさらに困ったことが起きます。どちらか一方のNANDが先に0を出力すると、それが他方のNANDの入力にもなり、他方のNANDは1出力になります。つまりQ=0なのか1なのか、どちらになるか確定しません。もはや記憶が正しいのか間違っているのかわからなくなってしまいます。この状態はセットかリセットをすれば解消はされますが、記憶する回路としては正しい動作にならないため、S=R=1の入力は禁止ということにする必要があります。
ということで、NAND型フリップフロップの動作を真理値表にまとめると以下のようになります。フリップフロップはNORでも構成でき、本質的は同じものになります。マイコンなどの電子回路や半導体にはフリップフロップが無数に実装されており、情報を一時的に記憶する機能で複雑な演算を行っています。フリップフロップとは”パタパタと変わる”というような意味合いだそうで、1と0がパタパタと変わる様子を表しているそうです。
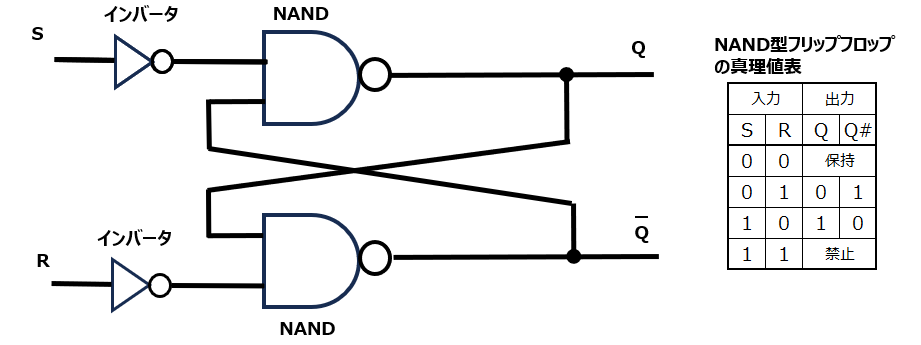
まとめ
情報を記憶できる最も基本的な回路構成であるフリップフロップについて解説いたしました。2つの入力があり、00(保持する)、01(リセットする)、10(セットする)、11(禁止)の4パターンがあり、保持する機能で情報を記憶できることがわかりました。複雑な電子回路も、このように記憶できる回路を無数に使って構成されています。